Basic Telecommunications Concepts

1: BASIC TELECOMMUNICATIONS CONCEPTS

1.1 What is Telecommunication?

Telecommunication means communicating over a distance using technology. The information can be in the form of voice, text, data, image, or video. In earlier days, communication was limited to letters and wired telegraph, but modern telecommunication uses electrical signals, optical signals, and radio waves to send information quickly over long distances.

In any telecommunication system, the information is first converted into a signal, then transmitted through a medium, and finally received and converted back into the original form.

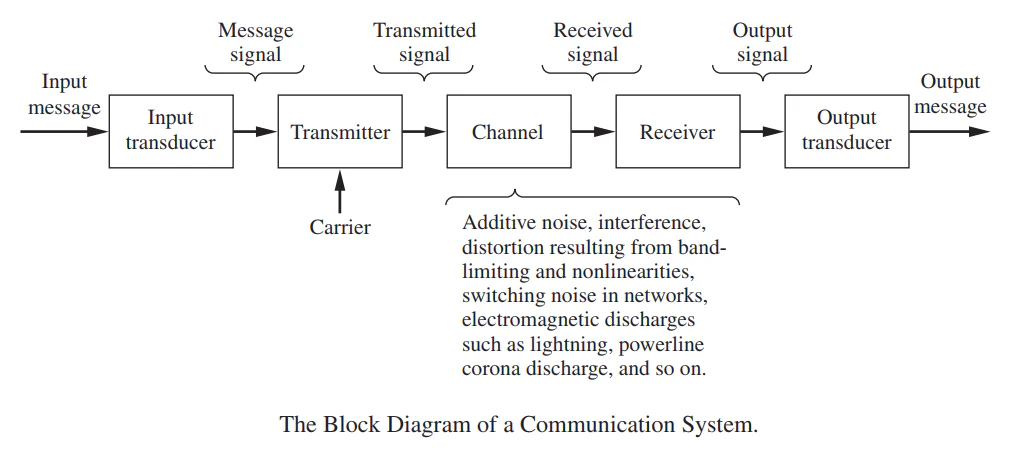
Explanation of Each Block

1. Information Source: This is the origin of the message. It can be a person speaking, a computer sending data, or a camera capturing an image.
2. Transducer: A transducer converts physical signals into electrical signals. For example, a microphone converts sound waves into electrical signals, and a camera sensor converts light into electrical signals.
3. Transmitter: The transmitter prepares the signal for transmission. It may amplify the signal, modulate it on a carrier, and encode it if the system is digital.
4. Channel: This is the path through which the signal travels. It can be a copper wire, optical fiber, or free space (air).
5. Noise: Noise is any unwanted disturbance that affects the signal during transmission. It can be due to thermal noise, interference from other signals, or electronic components.
6. Receiver: The receiver performs the reverse operations of the transmitter. It amplifies, demodulates, and decodes the received signal to recover the original message.
7. Output Transducer: It converts the electrical signal back into physical form, such as a speaker converting electrical signals into sound.
8. Destination: This is the final user who receives the information.

1.2 Types of Signals

Analog Signal

An analog signal is continuous in time and amplitude. This means its value can take any value within a range. For example, human speech and music are naturally analog. The main advantage of analog signals is that they represent natural signals accurately, but the disadvantage is that they are highly sensitive to noise and distortion.

Digital Signal

A digital signal has discrete values, usually represented as 0 and 1. Digital signals are widely used in modern communication systems because they are more resistant to noise, easy to store, and easy to process using computers and digital circuits. However, analog signals must first be converted into digital form before processing.

Other Classifications of Signals

1. Continuous and Discrete: Continuous signals exist at all time instants, while discrete signals exist only at specific time instants.
2. Energy and Power Signals: Energy signals have finite energy (e.g., a pulse), while power signals have finite power (e.g., a periodic sine wave).
3. Periodic and Aperiodic Signals: Periodic signals repeat after a fixed time, while aperiodic signals do not repeat.
4. Deterministic and Random Signals: Deterministic signals can be predicted exactly, while random signals (like noise) cannot be predicted.

2: SIGNAL PROCESSING

2.1 Meaning of Signal Processing

Signal processing is the field that deals with analyzing, modifying, and manipulating signals to improve their quality or to extract useful information from them. In telecommunication, signal processing is required because the signal gets distorted, weakened, or corrupted by noise during transmission.

The main objectives of signal processing are:

1. To remove noise and interference
2. To improve signal quality
3. To compress data for efficient transmission
4. To convert signals from one form to another (analog to digital and vice versa)

2.2 Important Operations in Signal Processing

(a) Filtering

Filtering is used to remove unwanted frequency components from a signal.

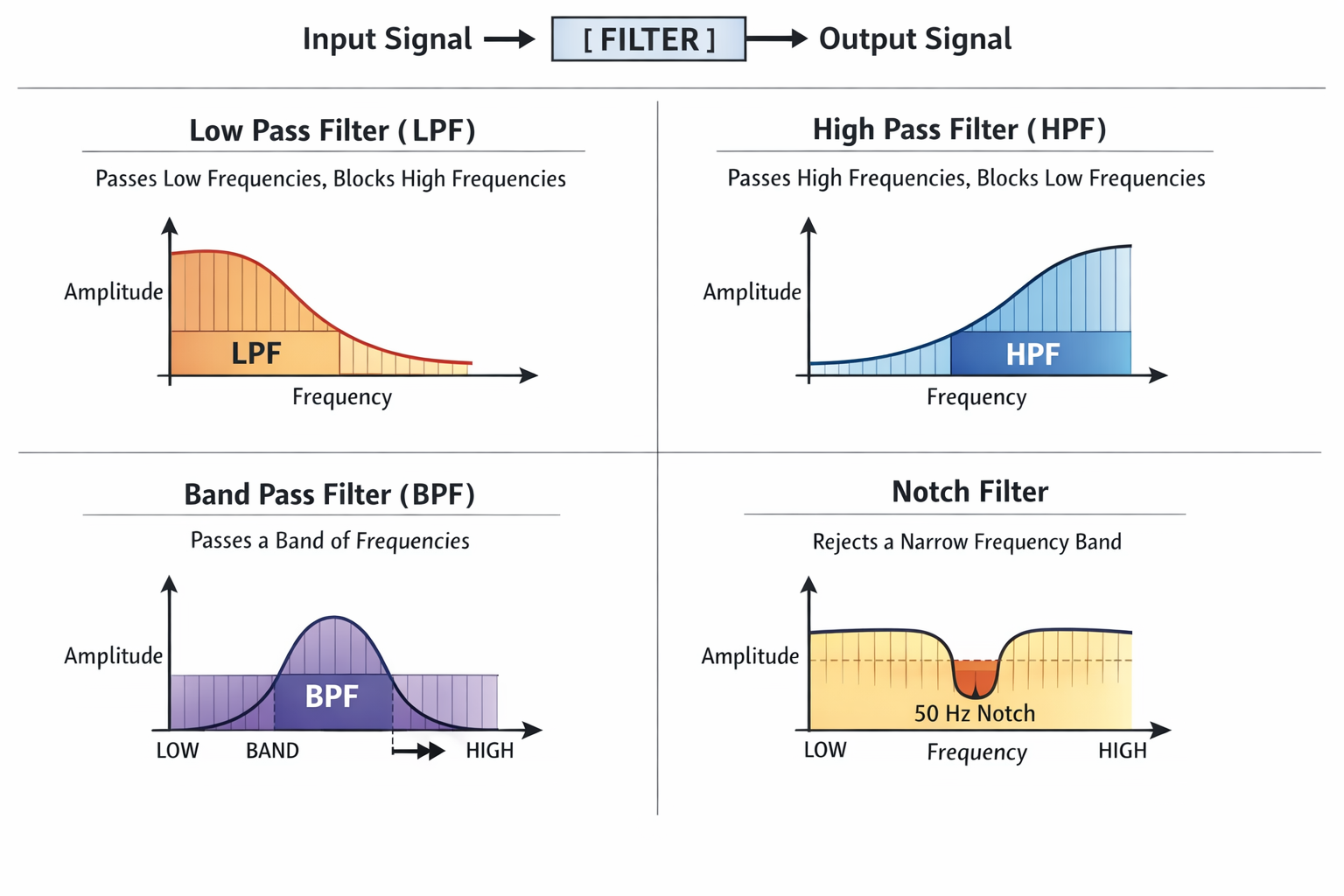
1. A Low Pass Filter (LPF) allows low-frequency components and blocks high-frequency components. It is often used to remove high-frequency noise.
2. A High Pass Filter (HPF) allows high frequencies and blocks low frequencies.
3. A Band Pass Filter (BPF) allows only a specific band of frequencies. This is useful in radio receivers to select a particular channel.
4. A Notch Filter removes a very narrow band of frequencies, such as 50 Hz power-line interference.

(b) Amplification

During transmission, signals become weak due to attenuation in the channel. An amplifier is used to increase the amplitude of the signal so that it can be processed or transmitted further.

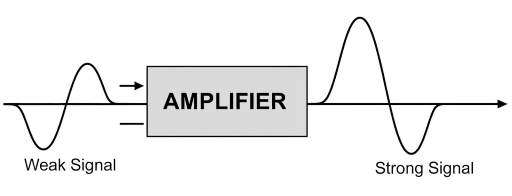
A good amplifier should increase strength without changing the shape of the signal, otherwise distortion occurs.

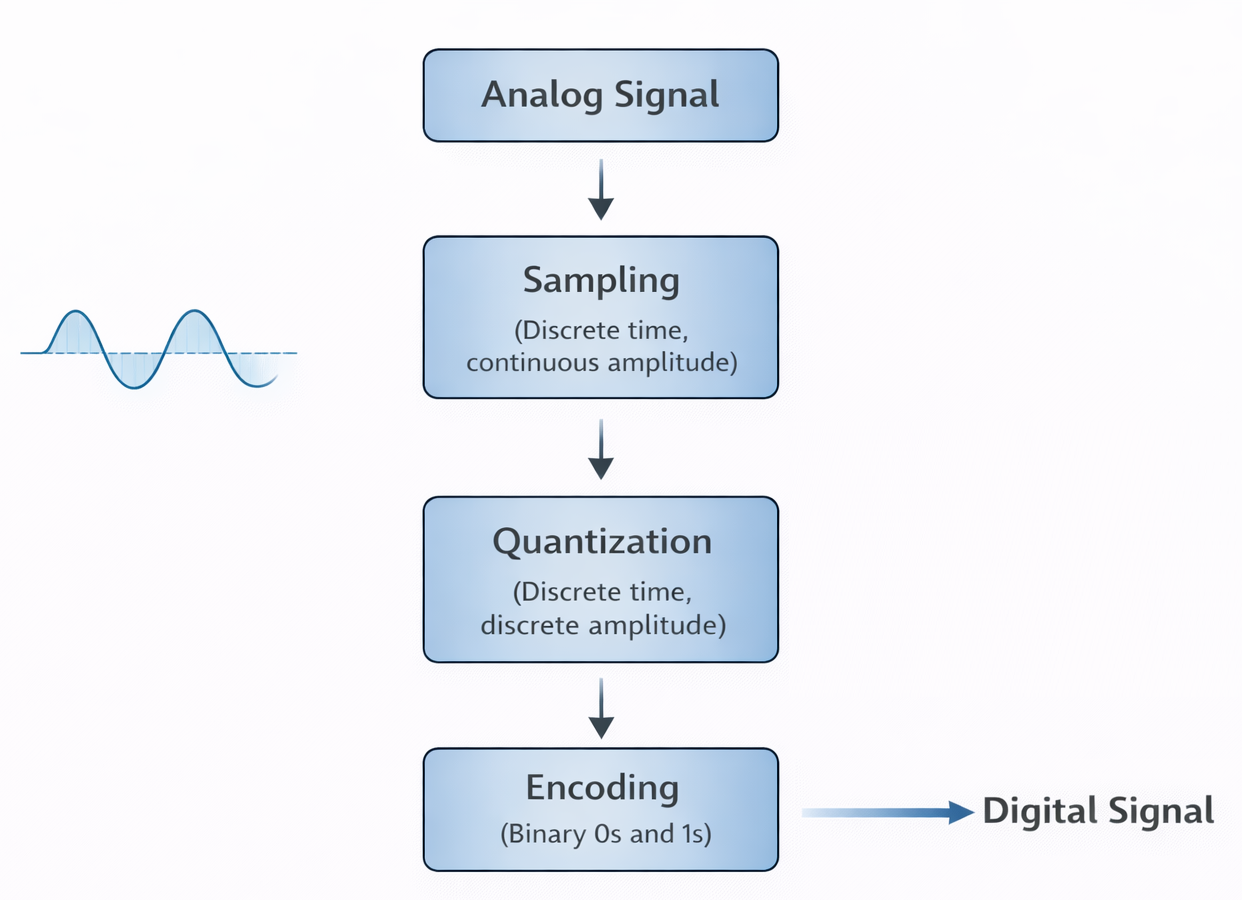
(c) Sampling

Sampling is the process of converting a continuous-time (analog) signal into a discrete-time signal by taking its values at regular intervals.

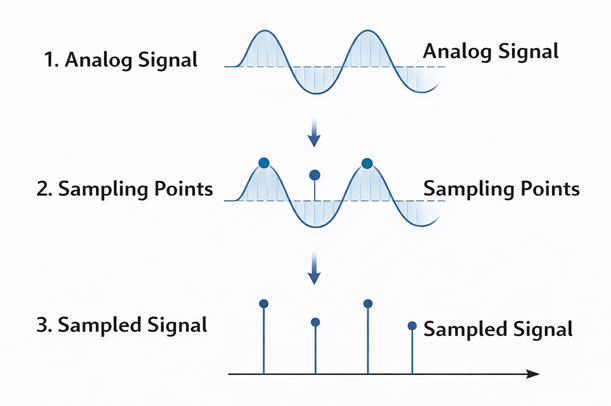
Nyquist Sampling Theorem states that the sampling frequency must be at least twice the highest frequency present in the signal. The minimum required sampling rate is called the Nyquist rate. If sampling frequency is less than Nyquist rate, aliasing occurs. Aliasing causes distortion and loss of information because high-frequency components appear as lower frequencies. To avoid aliasing, an anti-aliasing low-pass filter is used before sampling.

When we convert an analog signal (continuous in time) into a digital signal, we do this by sampling it at regular time intervals. The key question is: How fast should we sample the signal so that we can reconstruct it accurately later?

The sampling frequency ( fs​ ) must be at least twice the highest frequency component ( fmax​ ) present in the signal. Mathematically: fs≥ 2 fmax

Here:

1. fs = Sampling frequency (samples per second)
2. fmax = Highest frequency present in the input signal
3. 2 fmax is called the Nyquist rate

Why is “Twice the Highest Frequency” Necessary?

An analog signal is made up of many frequency components. To capture all the information in the signal, the sampling process must take enough samples per cycle of the fastest (highest frequency) component.

1. If you sample too slowly, you will miss important variations in the signal.
2. Sampling at at least twice the highest frequency ensures that every change in the signal is properly captured.
3. This makes it possible to reconstruct the original analog signal from the sampled data using a reconstruction filter.

In simple words: Sampling fast enough prevents different frequency components from getting mixed up.

What is Aliasing?

Aliasing is a distortion effect that occurs when the sampling frequency is less than twice the highest frequency of the signal.

When aliasing happens:

1. High-frequency components of the signal appear as lower-frequency components after sampling.
2. The sampled signal gives a wrong representation of the original signal.
3. This distortion cannot be removed later, even with filtering, because the information is already lost during sampling.

So, Aliasing causes loss of information and changes the shape of the signal.

An example to explain -

Suppose an analog signal contains frequencies up to 5 kHz.

1. According to Nyquist theorem, minimum sampling frequency should be:
2. fs ≥ 2×5 kHz=10 kHz = 10
3. If you sample at 10 kHz or more → Signal can be reconstructed correctly
4. If you sample at 6 kHz or 8 kHz → Aliasing will occur
5. The 5 kHz component will be misinterpreted as a lower frequency, and the reconstructed signal will be distorted.

How is Aliasing Prevented in Practice?

Before sampling, a Low Pass Filter (Anti-Aliasing Filter) is used:

1. It removes frequency components higher than fmax​.
2. This ensures that the signal satisfies Nyquist condition before sampling.
3. Then the signal is sampled safely without aliasing.

(d) Quantization

Quantization is the process of converting the continuous-amplitude sampled values into a finite number of discrete amplitude levels.

After sampling, the signal becomes discrete in time, but its amplitude is still continuous. This means that although we now take the signal values at specific time instants, each sampled value can still take any value within a range. However, digital systems cannot represent an infinite number of amplitude values. Therefore, the next step is quantization.

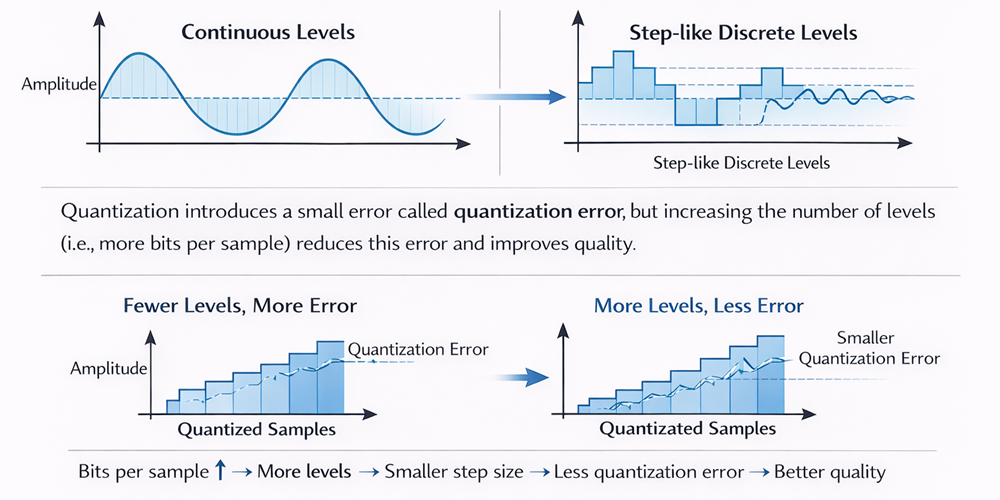
In quantization, the entire range of signal amplitude is divided into a fixed number of levels. Each sampled value is then rounded off to the nearest available level. As a result, the smooth waveform is converted into a step-like waveform.

Why Quantization is Needed

1. Digital systems can store and process only discrete values, not continuous ones.
2. Quantization makes the signal suitable for digital representation.
3. It is an essential step in converting an analog signal into a digital signal (ADC process).

Quantization Error

Because quantization approximates the actual sample value to the nearest level, a small difference appears between the original value and the quantized value. This difference is called quantization error.

Quantization error = Actual sample value − Quantized value

This error acts like a small amount of noise in the signal and slightly degrades the signal quality. This effect is known as quantization noise.

Effect of Number of Levels (Bits per Sample)

1. If we use more quantization levels (i.e., more bits per sample):
2. The step size becomes smaller
3. Quantization error reduces
4. Signal quality improves
5. If we use fewer levels (fewer bits):
6. The step size becomes larger
7. Quantization error increases
8. Signal quality degrades

More bits per sample → Better quality, but more data and higher bandwidth requirement.

(e) Encoding

After sampling and quantization, the signal becomes discrete in time and discrete in amplitude. However, these quantized values are still not in a form directly suitable for digital transmission or storage. Digital systems such as computers, digital switches, and communication networks work only with binary data (0s and 1s). Therefore, the next step is encoding.

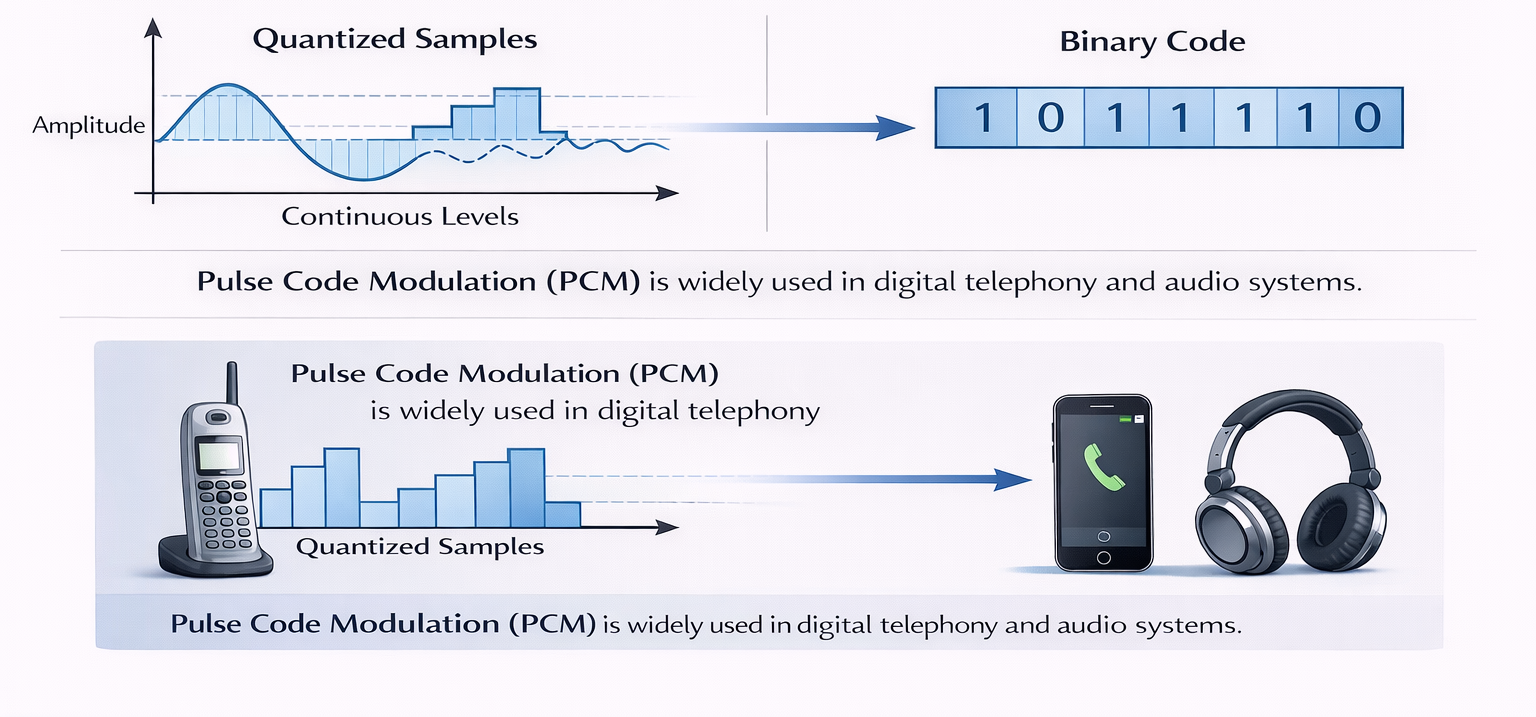
Encoding is the process of converting the quantized samples into binary form (0s and 1s).

In encoding, each quantization level is assigned a unique binary code word. As a result, every sample is represented by a group of bits, and the signal becomes a binary bit stream.

Why Encoding is Needed

1. Digital systems can store, process, and transmit only binary data.
2. Binary signals are more reliable in the presence of noise and interference.
3. Encoding makes the signal compatible with digital communication systems, computers, and digital storage devices.
4. It also allows the use of error detection and correction techniques to improve reliability.

How Encoding Works

1. Suppose the signal is quantized into a fixed number of levels.
2. Each level is given a binary number.
3. For example:
4. If there are 8 levels → 3 bits are needed (because 2^3=8)
5. If there are 16 levels → 4 bits are needed (because 2^4=16)
6. When a sample falls in a particular level, the corresponding binary code is transmitted
7. Thus, the output of the encoder is a sequence of 0s and 1s representing the original signal.

Pulse Code Modulation (PCM)

A very important and widely used encoding technique is Pulse Code Modulation (PCM).

In PCM:

1. The analog signal is sampled
2. The samples are quantized
3. The quantized values are encoded into binary form

PCM is widely used in digital telephony, audio CDs, and digital audio systems. It provides good noise immunity and allows easy digital processing and transmission of signals.